Bounding Rectangles
I was recently asked to assist in a project that was doing some Geo-mapping with Bing in an extension application to Dynamics CRM.
But, first the disclaimer… I am neither a geometrist nor cartographer, so please be kind if I get some of the minutia details off a little.
The basic functionality that they were trying to accomplish goes something like this:
The user will select a pre-built Advanced Find query for selecting some Accounts. The results show in a standard table grid display.
As the user selects an Account and adds it to their Route, a couple things happen on the Bing map:
a) All of the, thus far, selected Accounts in the route each have their pushpin displayed.
b) All other Accounts, that are owned by the user, that are within a “proximity” to those Accounts should also show on the map, with a different style pushpin to differentiate them. Let’s call these “Candidate Accounts”.
The mechanism that they are using for “proximity” is a rectangular boundary that is 5 miles larger (in all directions) than a rectangle that would be naturally made by the furthest Top, Left, Bottom, Right of the Accounts in the current Route.
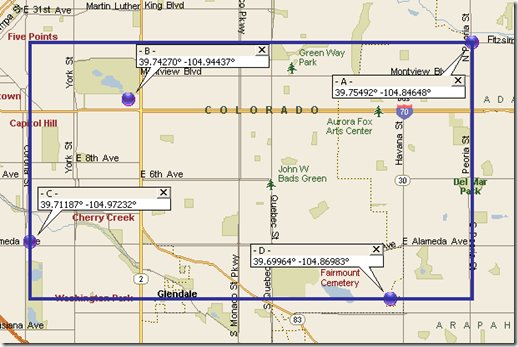
Let’s look at a picture that represents the (a) bullet above: Four selected Accounts:
Here we have 4 Accounts in our Route (Purple Circles). Notice how a rectangle can be represented by the four points that represent the:
- Furthest Top (A)
- Furthest Left (C)
- Furthest Bottom (D)
- Furthest Right (A)
Also note that the Account in the top-right corner (A) happens to be both the Furthest Top and the Furthest Right, while the Furthest Left (C) and Furthest Bottom (D) are two different Points.
Now, before we can perform step (b) to show our Candidate Accounts, we have to expand our rectangular area by 5 miles to define our “proximity”. We want to pick up the Accounts of Interest that are within 5 miles outside of our current purple rectangle.
First, for a quick review of Longitude and Latitude you may want to check our this Wikipedia Article. Since most digital mapping systems can use decimal degrees, we will do everything in decimal degrees and most people can work just fine with decimal numbers. But, the one thing I see most people stumble over the most, is remembering which measurement is for which direction. So, here’s a simple rule:
- Latitude is the measurement that runs North and South on the Globe. (Think ‘rhymes with altitude, as in “up and down” as in Vertical.)
- Longitude is the measurement that runs East and West on the Globe. (Think aLONG the Equator as in Horizontal.)
And, for our geometry review, recall that we only need 2 points on the plane to draw a rectangle. By convention, this is usually the Top-Left corner and the Bottom-Right corner. So we will use those two points.
Here are the point coordinates for our four Accounts as mapped above along with the minimums and maximums of those coordinates.
Point Latitude Longitude - A - 39.75492 -104.84648 - B - 39.74270 -104.94437 - C - 39.71187 -104.97232 - D - 39.69964 -104.86983 Min 39.69964 (D) -104.97232 (C) Max 39.75492 (A) -104.84648 (A)
To calculate our two points, we need to find the minimum and maximum of our data. The formula for determining our two points is as follows:
- Top-Left = ( Max(Latitude), Min(Longitude) )
- Bottom-Right = ( Min(Latitude), Max(Longitude) )
And when we substitute our actual numbers from our table, we end up with:
- Top-Left = (39.75492, -104.97232)
- Bottom-Right = (39.69964, -104.84648)
Let’s plot these points to make sure we have the math correct:
Now we have the two points that define our original rectangle around our original four Accounts as shown by the red pushpins.
So-far, so-good. That wasn’t too hard.
But, now we need to move our two points 5 miles in EACH of the four directions: North, South, East, West
Up to know, we have had a mapping lesson, a geometry lesson, and now it’s time for a trigonometry lesson.
Let’s zoom into our Bottom-Right corner:
We need to move the Bottom-Right corner both East (side a) and South (side b) by 5 miles. (note that the above picture is a smaller scale of only .5 miles) This means that we need to move the Bottom-Right point along the purple line (side c).
Distance Between Two Known Points
Does anyone remember the formula? Anyone remember the Pythagorean theorem? Here we go:
And substituting our numbers we get:
Well, that sure seems easy enough. The problem lies in the basic question of: how do we convert the unit of miles into longitude-latitude?
This gets even more complicated by the fact that, contrary to popular belief, the earth is not flat! Realizing that this is still a controversial topic for some, we live on a spherical ball! And worse, it’s not even a perfect sphere. It’s a little uneven in spots. The smart people (of which I’m not) call it an ablate spheroid.
Basically, we are talking about calculating the distance between points on the planet. There is an excellent, understandable presentation of the math involved over here at Meridian World Data. They present three approaches to the problem. Rough Approximation, Improved Approximation, Great Circle Distance.
For our requestor’s situation, it was decided to use the Improved Approximation formula:
Improved approximate distance in miles:
c = sqrt( a * a + b * b )
where a = 69.1 * (lat2 - lat1)
and b = 69.1 * (lon2 - lon1) * cos(lat1/57.3)
Unfortunately, the problem we have with this formula is that it is the difference between two known points. But, in our situation, we only have ONE known point and we already know the distance (5 miles).
Known Point + Miles = New Point
There is a fantastic and succinct blog explaining how to perform this conversion over at The Endeavour by John D. Cook.
As we mentioned above, let’s assume the earth is a perfect sphere and that at the equator the radius (R) is:
R = 3960.0 miles
And because it is a sphere, a “line” is actually an arc along the circumference of the sphere.
Also of import is the fact that all the math and angles on a sphere are in Radians and/or results are in Radians. But, Longitude and Latitude are all in Decimal Degrees. Thus, we need to know how to convert between them:
The formulae for converting between Degrees and Radians are:
Degrees = Radian * (180 / PI)
Radians = Degrees * (PI / 180)
Using these formulae, we can define our conversion constants as thus:
RadiansToDegrees = (180 / PI)
DegreesToRadians = (PI / 180)
Moving North and South
The formula for the change in distance North and South along a Latitude is:
DistanceNorthSouth = (MilesToMove / RadiusAtEquator) * RadiansToDegrees
Note that (MilesToMove / RadiusAtEquator) will give us the arc distance in Radians. But, we will need it in Degrees since Longitude and Latitude are in Decimal Degrees. Which is why we have to multiply by RadiansToDegrees to get us to Degrees.
Moving East and West
The formula for the change in distance East and West along a Longitude is more complicated. As we discussed, this is because as we get closer to either of the earth’s poles, the distance that one degree of longitude represents gets smaller and smaller. In fact, a circle parallel to the equator, is cos(x) times smaller than the circumference at the equator.
To make this easier, let’s do this in two parts.
First, we need to find the radius (r) of the earth at the latitude that we need to move East or West on.
RadiusAtLatitude = RadiusAtEquator * cos( LatitudeDecimalDegrees * DegreesToRadians )
Now, we can use the same basic formula we used for North and South, but now use the radius (r) for where we actually are on the earth:
DistanceEastWest = (MilesToMove / RadiusAtLatitude) * RadiansToDegrees
Move Point, Move!
We are almost at the finish line!
Now that we know how to convert our Miles to a Decimal Degrees, we can now calculate our new points. And, let’s combine all our steps into single formulae to simplify the implementation in your own language.
NewTopLatitide = StartingLatitude + (MilesToMove / 3960) * (180/PI)
NewLeftLongitude = StartingLongitude - (MilesToMove / (3960 * COS(LatitudeDecimalDegrees * (PI/180)))) * (180/PI)
NewBottomLatitude = StartingLatitude – (MilesToMove / 3960) * (180/PI)
NewRightLongitude = StartingLongitude + (MilesToMove / (3960 * COS(LatitudeDecimalDegrees * (PI/180)))) * (180/PI)
Ok, let’s do the math…
Recall that our starting rectangle’s two points are:
- Top-Left = (39.75492, -104.97232)
- Bottom-Right = (39.69964, -104.84648)
And when we plug in those points and use 5 miles for our MilesToMove, we end up with these new points:
- New-Top-Left = (39.82726, -105.06642)
- New-Bottom-Right = (39.62730, -104.75246)
Which, when we plot on our map, and add some measurement lines to validate our results, we get exactly what we are looking for: A new rectangle that is exactly 5 miles farther out, in all directions, from our original rectangle.
Summary
WOW, That was a blast. We got a review of several math disciplines: Geometry, Algebra, Trigonometry. We got to play with cool pictures of maps and some pretty colors. What more could a person ask for.
We learned a little bit about how Longitude and Latitude work, and the complications of shrinking distances on Longitude as you move towards either of the earth’s poles.
And ultimately, we were able to answer the question of how to move a (Longitude,Latitude) point on a map a specified distance in miles (5 miles in our case).
I hope that you have had as much fun learning this as I did in my original research!
Robert
- One is pleased to be of service





No comments:
Post a Comment